 |
|
| |
| |
 微積分基本定理》 微積分基本定理》 |
|
| |
範例 17:四邊形面積公式及微積分基本定理 |
|
| |
三角形被三個邊長完全確定,四邊形則否,有名的海龍公式告訴我們如何利用三個邊長來計算三角形的面積,至於四邊形求面積的公式,你知道怎麼利用微積分基本定理導出來嗎?
|
|
| |
《 解答
》 |
|
|
| |
|
| |
|
| |
| |
| |
 微積分基本定理》 微積分基本定理》 |
|
| |
範例 18:工人拉船 |
|
| |
碼頭上,有一個圓筒狀鐵柱,從船上拋出一根繩子,一端固定在船尾,另一端繞鐵柱三圈後由一工人拉著,假設工人施力10公斤,繩子與鐵柱的磨擦係數是1/3,請問船尾受力多大?
|
|
| |
《 解答
》 |
|
|
| |
|
| |
|
| |
| |
| |
 積分問題》 積分問題》 |
|
| |
範例 19:總統副總統喝咖啡問題 |
|
| |
總統與副總統一同坐下來喝咖啡,他們面前各有一杯相同溫度的咖啡,總統先勺了一匙奶精加到咖啡內攪拌均勻。過了十分鐘後,副總統也加入相同份量的奶精(注意:奶精一直保持相同的溫度)並且攪拌均勻。隨後兩人同時喝咖啡,假設奶精的溫度比室溫低,室溫又比咖啡低,那麼誰喝到較熱的咖啡?
|
|
| |
《 解答
》 |
|
|
| |
|
| |
|
| |
| |
| |
 積分問題》 積分問題》 |
|
| |
範例 20:Mercator地圖 |
|
| |
Mercator地圖是由G. Mercator在1569年所提出,至今在航海上仍廣為使用,你想知道Mercator地圖和微積分的關係嗎?
|
|
| |
《 解答
》 |
|
|
| |
|
| |
|
| |
| |
| |
 積分問題》 積分問題》 |
|
| |
範例 21:雨中行車 |
|
| |
若你駕駛一輛風玻璃與地面垂直的吉普車欲從甲地到乙地,此時天正下著雨,假設所有雨滴皆以速度
u 垂直落下,且均勻的分布在空氣中,請問你是該開的快一點或是慢一點,才能使落在擋風玻璃的雨水總量最少?
|
|
| |
《 解答
》 |
|
|
| |
|
| |
|
| |
| |
| |
 積分問題》 積分問題》 |
|
| |
範例 22:錄音帶 |
|
| |
如果你曾注意過收音機帶動錄音帶的情形,相信你會發現在收聽(或者快轉)的時候,在左方的輪子會逆時針旋轉,以帶動磁帶,而原本在右方的磁帶地方就會被一直帶動,最後會繞到左方的輪子上。
現在我們考慮二個問題:兩個輪子磁帶半徑的變化率之比為多少? 如果我知道錄音帶從一開始(左方的輪子沒有磁帶,所有磁帶都在右方的輪子上)轉到一半
(左方的磁帶量=右方的磁帶量)時,需要一分鐘,並且輪 1 的轉速始終保持一定值,那麼錄音帶全部轉完的時候需要幾分鐘呢?
|
|
| |
《 解答
》 |
|
|
| |
|
| |
|
| |
| |
| |
 積分問題》 積分問題》 |
|
| |
範例 23:撞球問題 |
|
| |
你知道撞球的時候球桿應該打在哪裡最好嗎?
|
|
| |
《 解答
》 |
|
|
| |
|
| |
|
| |
| |
| |
 積分問題》 積分問題》 |
|
| |
範例 24:n!的近似公式 |
|
| |
對於n!=1 × 2 ×‧‧‧× n 這個數,你是一個數一個數乘呢?還是可以一次算出來它大概是多少呢?由Stirling的近似公式可以幫助你很快地算出它的近似值喔!
|
|
| |
《 解答
》 |
|
|
| |
|
| |
|
| |
| |
| |
 積分問題》 積分問題》 |
|
| |
範例 25:兩個無理數的證明 |
|
| |
在BBS的 math版中,常常會看到有人問 : 為什麼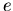 是無理數呢?π是無理數嗎?你知道為什麼嗎? 是無理數呢?π是無理數嗎?你知道為什麼嗎?
|
|
| |
《 解答
》 |
|
|
| |
|
| |
|
| |
| |
| |
 積分問題》 積分問題》 |
|
| |
範例 26:牛吃草問題 |
|
| |
有一頭牛,被栓在一個半徑為 r 的木椿上(如下圖所示)繩子的一端被固定在A點,而牛能夠走到木椿的對面B。木椿的外部都是草地,請問牛有辦法吃到多少草呢?
|
|
| |
《 解答
》 |
|
|
| |
|















