| |
 |
| |
 |
|
|
 |
| |
| |
 積分問題》 積分問題》 |
|
| |
範例 20:Mercator地圖 |
|
| |
Mercator地圖是由G. Mercator在1569年所提出的。至今在航海上仍廣為使用,在Mercator地圖中,經度差相同的經線被攤開為平面上距離相同的平行線。而緯線在地圖上為與經線垂直的直線,而且Mercator
地圖在水平方向和垂直方向的縮收比例一樣。
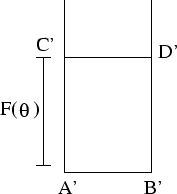
圖一為地球的一部分,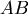 為赤道, 為赤道,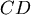 為緯度為θ的緯線,假設地球為半徑為 1,圖二為地球的 Mercator地圖, 為緯度為θ的緯線,假設地球為半徑為 1,圖二為地球的 Mercator地圖,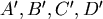 分別對應 分別對應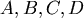 ,若 ,若 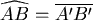 ,則 ,則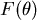 =? =?
| 圖一 |
圖二 |
 |
 |
|
|
| |
《 解答 》 |
|
| |
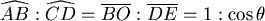 , ,
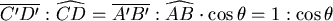
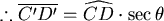 。緯度θ時,地圖水平與垂直上的縮放率為
secθ, 。緯度θ時,地圖水平與垂直上的縮放率為
secθ,
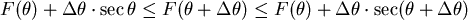
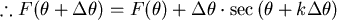 , ,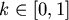 (中間值定理) (中間值定理)
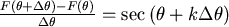 ,當 ,當 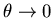 時, 時,
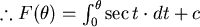 。又 。又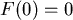 ,所以 ,所以 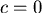 , ,
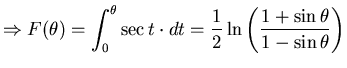
,當 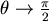 , ,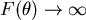 。這表示 Mercator 地圖無法在有限的紙上畫出完整的地球,而緯度θ時縮放比例為 secθ,secθ為遞增函數。這說明Mercator地圖在緯度越高時失真的情形便越嚴重。 。這表示 Mercator 地圖無法在有限的紙上畫出完整的地球,而緯度θ時縮放比例為 secθ,secθ為遞增函數。這說明Mercator地圖在緯度越高時失真的情形便越嚴重。
另外值得一提的是,將地球投影至Mercator地圖上其實是一個保角變換,所謂保角,指的是任兩條曲線的夾角經變換後仍保持不變。正由於Mercator地圖保持角度,使得其在航海上有一重要的應用。Mercator地圖上的直線在地球上對應的曲線一般稱為斜駛線
(Loxodromic Curve)或羅盤方位線。由於Mercator地圖上的直線與經線皆保持固定夾角,所以斜駛線與經線的夾角也保持固定。如果欲從地球上的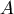 點航行到 點航行到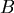 點,可先找到 點,可先找到 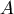 , , 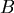 在Mercator地圖上對應的 在Mercator地圖上對應的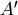 , , 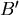 ,若地圖上的直線 ,若地圖上的直線
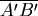 與經線的夾角為θ,則在航行時只要將羅盤角度固定與經線一直保持θ角,便可以從 與經線的夾角為θ,則在航行時只要將羅盤角度固定與經線一直保持θ角,便可以從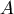 沿著斜駛線到達 沿著斜駛線到達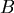 了。雖然斜駛線一般來說並不是最短距離,但沿著斜駛線行駛卻是個不易迷路的好方法。 了。雖然斜駛線一般來說並不是最短距離,但沿著斜駛線行駛卻是個不易迷路的好方法。
附註: 根據岩波數學辭典260.D條,如果球面半徑為1,經度是 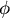 ,緯度是θ,則Mercator
map: ,緯度是θ,則Mercator
map:
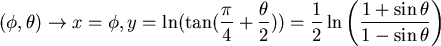
因此,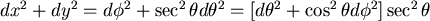 是保角變換。 是保角變換。
|
|
| |
|
|
| |
About This
document |
|
| |
This document was
generated using the LaTeX2HTML
translator Version 2K.1beta (1.47)
Copyright © 1993, 1994, 1995, 1996, Nikos
Drakos, Computer Based Learning Unit, University
of Leeds.
Copyright © 1997, 1998, 1999, Ross
Moore, Mathematics Department, Macquarie University,
Sydney.
The command line arguments were:
latex2html -local_icons -white -notransparent
canswer18-html.tex
The translation was initiated by Shu Cheng-chou
on 2003-05-14
|
|
|
| |
|
| |
|
|
| |
|
 |















