| 三角形被三個邊長完全確定,四邊形則否。有名的海龍公式告訴我們如何利用三個邊長來計算三角形的面積。至於四邊形求面積的公式,不能只用四個邊長,還要加上頂角的角度,公式由
Bretschneider 在 1842提出(註一)。如果四個邊長依序為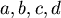 ,而相關的頂角分別為 ,而相關的頂角分別為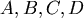 (如圖一) (如圖一)
 |
圖一 |
則此四邊形的面積 的平方可以表為 的平方可以表為
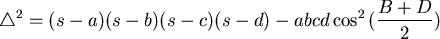 其中
其中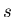 是周長的一半,如果以 是周長的一半,如果以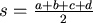 代入整理, 代入整理,
可以將Bretschneider公式寫成:
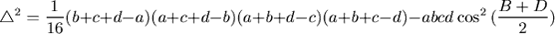
一個重要的結果是,當此四邊形內接於一個圓的時候,由於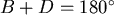 ,因此面積會最大,並且面積的平方就是 ,因此面積會最大,並且面積的平方就是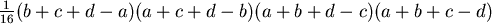 。有關Bretschneider公式,蔡聰明在他的書中用平面幾何的方法給了完整的證明(同註一)。本文嘗試用微積分的方法來得出相同的公式,想法來自微積分基本定理–我們想要求一個圖形的面積,不妨把面積對某個參數微分,看看能得出什麼,然後再積分(反微分)回去,積分回去的時候,會生出一個不定常數,再想方法確定這個常數,在本文中,四邊形的四個邊長 。有關Bretschneider公式,蔡聰明在他的書中用平面幾何的方法給了完整的證明(同註一)。本文嘗試用微積分的方法來得出相同的公式,想法來自微積分基本定理–我們想要求一個圖形的面積,不妨把面積對某個參數微分,看看能得出什麼,然後再積分(反微分)回去,積分回去的時候,會生出一個不定常數,再想方法確定這個常數,在本文中,四邊形的四個邊長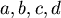 給定,它的面積以 給定,它的面積以 表示(如圖二所示),參數就是角 表示(如圖二所示),參數就是角 ,至於角 ,至於角 ,它被 ,它被 所決定,因此可以看成 所決定,因此可以看成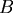 的函數。 的函數。
 |
圖二 |
我們先把 寫成 寫成
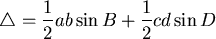
則有
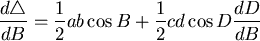
因為
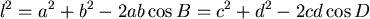
微分之後有
 |
(1) |
現考慮
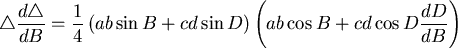
將(1)代入得
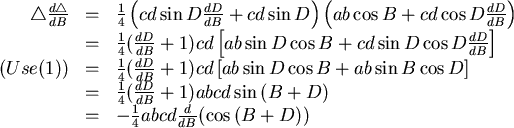
所以
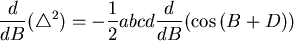
因此
 |
(2) |
其中
 是一個待定的常數。 是一個待定的常數。
如何決定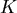 ,當然要選一個特別的角 ,當然要選一個特別的角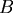 代入,一般會想到讓 代入,一般會想到讓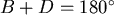 ,此時 ,此時 就是內接於一圓時四邊形的面積,但這未必好求。比較好的方法是令 就是內接於一圓時四邊形的面積,但這未必好求。比較好的方法是令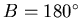 ,四邊形就變成了一個三角形。(如圖三) ,四邊形就變成了一個三角形。(如圖三)
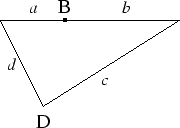 |
圖三 |
這雖然是一個退化的情形,但是一則不影響一般性,再則三角形的面積有現成的海龍公式,也就是說我們得到
 |
(3) |
再用一次餘弦定律
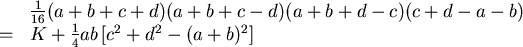 |
(4) |
我們注意左邊就是三角形三邊長為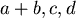 的面積平方(海龍)公式。 (4)式已經決定了 的面積平方(海龍)公式。 (4)式已經決定了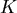 ,雖然尚未整理,卻至少告訴我們, ,雖然尚未整理,卻至少告訴我們,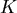 是一個 是一個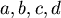 的四次齊次多項式。 的四次齊次多項式。
現在,可以利用配方來整理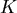 (這需要一點後見之明) (這需要一點後見之明)
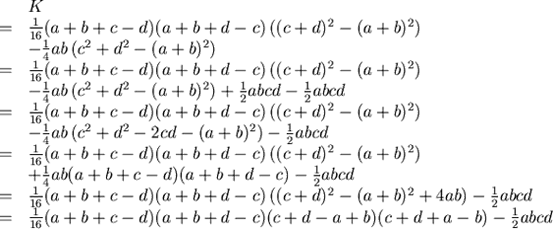
代回到(2)
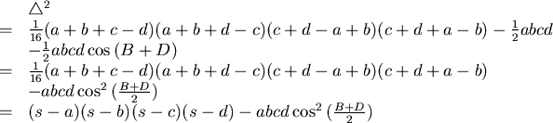
這是Bretschneider公式。
我第一次看到將 對角 對角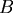 微分,是在項武義老師的演講中,他的講題是等周問題(Isoperimetric
Problem), 他寫下了 微分,是在項武義老師的演講中,他的講題是等周問題(Isoperimetric
Problem), 他寫下了
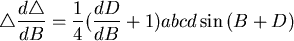
然後,他令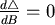 ,得出 ,得出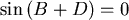 或者 或者 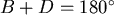 時, 時, 會有最大值。他利用這個事實嘗試給等周問題一個比較幾何的證明(當然,他假設了等周問題是有解的)(註二)他的證明如下:不妨假設這個面積最大的情形是發生在一個凸的區域(周長給定)(如圖四) 會有最大值。他利用這個事實嘗試給等周問題一個比較幾何的證明(當然,他假設了等周問題是有解的)(註二)他的證明如下:不妨假設這個面積最大的情形是發生在一個凸的區域(周長給定)(如圖四)
 |
圖四 |
任取四點,連一個四邊形,如果ABCD不能內接於一圓,那麼就可以調整角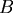 ,讓ABCD的面積更大,而注意到作這個調整的時候弧長AB,BC,CD及DA都沒有改變。因此,如果這個凸區域在給定的周長之下具有最大面積的話,那在邊上任取四點,所成的四邊形都必須內接於一圓,不難證出這些圓根本就是同一個圓,這個凸區域就是此圓的內部。等周問題主張在周長一定的時候,圓域的面積最大。武義師的證明相當有啟發性。(註三) ,讓ABCD的面積更大,而注意到作這個調整的時候弧長AB,BC,CD及DA都沒有改變。因此,如果這個凸區域在給定的周長之下具有最大面積的話,那在邊上任取四點,所成的四邊形都必須內接於一圓,不難證出這些圓根本就是同一個圓,這個凸區域就是此圓的內部。等周問題主張在周長一定的時候,圓域的面積最大。武義師的證明相當有啟發性。(註三)
註一:見蔡聰明,數學的發現趣談,三民書局九十一年版,第163頁。
註二:等周問題是問,當周長一定的時候,什麼樣的區域會有最大的面積。答案是圓域,有興趣的讀者可以參考Courant
and John, Introduction to Calculus and Analysis,
Vol II, p.p. 365-366。
註三:八十八年項武義在台大數學系給的演講。
|















