| |
 |
| |
 |
|
|
 |
| |
| |
 向量微積分》 向量微積分》 |
|
| |
範例 50:阿基米德原理 |
|
| |
你知道什麼是「阿基米德原理」嗎?你想知道如何理解阿基米德原理嗎?
|
|
| |
《 解答 》 |
|
| |
其中 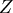 是 是 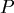 點的 點的 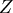 座標, 座標,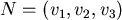 是 是 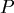 點指向體 點指向體 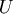 之外的單位長法向量,把表面 之外的單位長法向量,把表面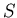 所承受的壓力作一面積分,以 所承受的壓力作一面積分,以
表示,注意這是一個向量值的積分,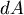 是 是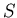 的面積元素(area element) 的面積元素(area element)
我們可以利用Stokes定理來把上面這個面積分改寫成一個體積分
(定理: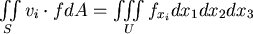 )所以 )所以
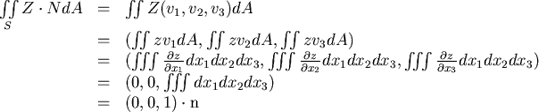
這裡,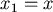 , , , ,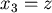 , n代表U的體積。 , n代表U的體積。
我們也可以避開Stokes定理,直接理解 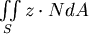 。 。 由投影的觀點,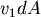 , ,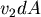 , ,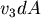 分別是 分別是 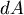 在 在  平面, 平面,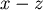 平面, 平面,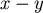 平面的投影。 平面的投影。
先看 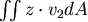
在曲面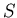 上取一點 上取一點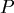 ,經 ,經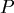 點沿 點沿 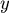 軸方向,作一射線,交 軸方向,作一射線,交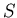 於另一點 於另一點 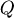 ,則 ,則 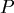 和 和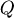 的 的  坐標相等,而 坐標相等,而 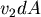 的大小都是 的大小都是 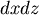 ,但是因為 ,但是因為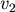 在 在 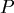 和 和 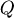 的符號相反,因此 的符號相反,因此
這裡證明了 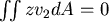 ,同理 ,同理 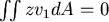 再看 再看 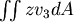 , ,
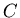 點沿 點沿  軸的方向作一射線,交 軸的方向作一射線,交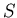 於另一點 於另一點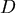 ,在 ,在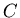 和 和 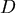 , , 坐標的差額是 坐標的差額是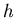 ,再乘上 ,再乘上 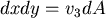 作積分,就得到物體 作積分,就得到物體 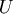 的體積 的體積
註:施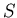 表面的力對區域 表面的力對區域 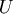 的幾何中心(或 的幾何中心(或 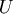 這塊水的質心)的總力矩也等於 0,即若將質心置於原點的話,可以證得 這塊水的質心)的總力矩也等於 0,即若將質心置於原點的話,可以證得
|
|
| |
|
|
| |
About This
document |
|
| |
This document was
generated using the LaTeX2HTML
translator Version 2K.1beta (1.47)
Copyright © 1993, 1994, 1995, 1996, Nikos
Drakos, Computer Based Learning Unit, University
of Leeds.
Copyright © 1997, 1998, 1999, Ross
Moore, Mathematics Department, Macquarie University,
Sydney.
The command line arguments were:
latex2html -local_icons -white -notransparent
canswer03-html.tex
The translation was initiated by Shu Cheng-chou
on 2003-05-13 |
|
|
| |
|
| |
|
|
| |
|
 |















