| |
 |
| |
 |
|
|
 |
| |
| |
 微分》 微分》 |
|
| |
範例 44:行星繞日的軌道 |
|
| |
在萬有引力的作用下,為什麼行星繞日的軌道是圓錐曲線呢?
|
|
| |
《 解答 》 |
|
| |
假設行星的位置坐標寫成 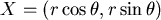 ,速度 ,速度 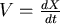 , ,
計算 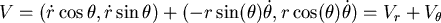
其中 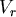 表方向的速度, 表方向的速度,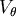 表垂直方向的速度, 表垂直方向的速度,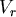 的大小是 的大小是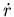 , ,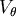 的大小是 的大小是 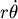
角動量守恒表示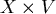 是常數,它的大小是 是常數,它的大小是 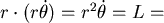 常數, 常數,
令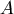 表示加速度向量 表示加速度向量 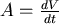 ,它指向太陽﹙原點﹚大小與 ,它指向太陽﹙原點﹚大小與 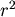 成反比。 成反比。
計算
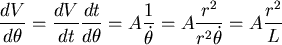
因此 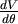 的方向指向原點,並且大小固定。 的方向指向原點,並且大小固定。
令 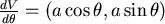 , ,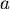 是常數。 是常數。
因此 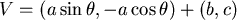 ; ;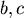 是常數。 是常數。
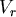 的大小 = 的大小 = 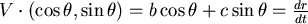 ,除以 ,除以 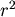
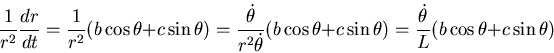
所以 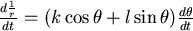 , ,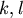 是常數,亦即 是常數,亦即
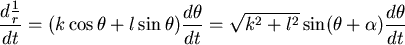
不妨設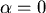 ,得 ,得  , ,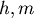 是常數 是常數
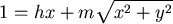
或
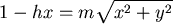
兩邊平方,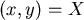 滿足錐線方程。 滿足錐線方程。
註:注意到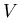 分佈在以 分佈在以 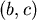 為心,半徑為 為心,半徑為 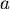 的圓上, 的圓上,
這對軌道是圓錐曲線有什麼幾何直觀的提示呢?
|
|
| |
|
|
| |
About This
document |
|
| |
This document was
generated using the LaTeX2HTML
translator Version 2K.1beta (1.47)
Copyright © 1993, 1994, 1995, 1996, Nikos
Drakos, Computer Based Learning Unit, University
of Leeds.
Copyright © 1997, 1998, 1999, Ross
Moore, Mathematics Department, Macquarie University,
Sydney.
The command line arguments were:
latex2html -local_icons -white -notransparent
canswer37-html.tex
The translation was initiated by Shu Cheng-chou
on 2003-05-21
|
|
|
| |
|
| |
|
|
| |
|
 |















