| |
 |
| |
 |
|
|
 |
| |
| |
範例 38:溜滑梯(最速下降曲線) |
|
| |
一個小圓盤,由A點往下滑到B點,該以何種路徑往下滑,所花費的時間最短呢?
|
|
| |
《 解答 》 |
|
| |
假設A、B兩點之間無摩擦力,如果路徑如下圖:
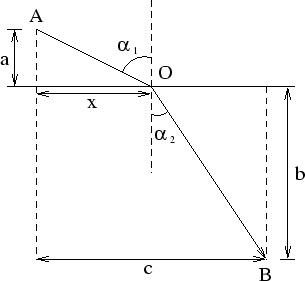
小球由A到O的速度是 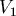 ,由O到B的速度是 ,由O到B的速度是 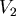 ,則從A到B所花的時間 ,則從A到B所花的時間
因為要求最短時間,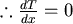
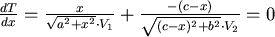
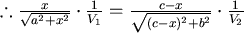
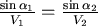 如果路徑變成如下: 如果路徑變成如下:
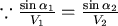
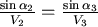
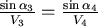
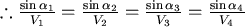
如果將A、B之間愈切愈細,則可以發現,在每一點會有 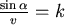 , ,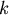 是一個常數。 是一個常數。
又在每一點的 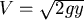 , , 向下為正。 向下為正。
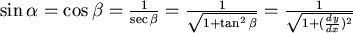
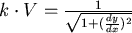
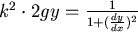 ,let ,let 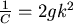
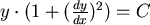
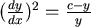
現在讓 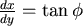 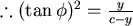
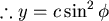
則 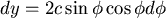
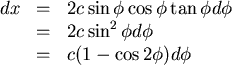
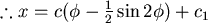
又有初始條件 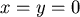 ,as ,as 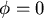
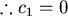
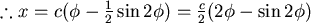
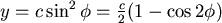
Let 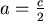 , ,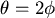 則 則 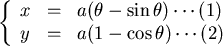
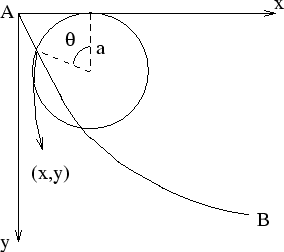
又: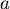 被B點的坐標 被B點的坐標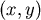 決定。 決定。
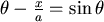
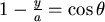
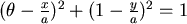
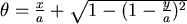
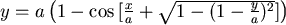
∴ 當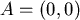 ,不同的B點位置會決定不同的 ,不同的B點位置會決定不同的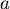 值。 值。
註:這種曲線稱為 cycloid。
|
|
| |
|
|
| |
About
This document |
|
| |
This document
was generated using the LaTeX2HTML
translator Version 2K.1beta (1.47)
Copyright © 1993, 1994, 1995, 1996, Nikos
Drakos, Computer Based Learning Unit, University
of Leeds.
Copyright © 1997, 1998, 1999, Ross
Moore, Mathematics Department, Macquarie
University, Sydney.
The command line arguments were:
latex2html -local_icons -white -notransparent
canswer23-html.tex
The translation was initiated by Shu Cheng-chou
on 2003-05-19
|
|
|
| |
|
| |
|
|
| |
|
 |















