| |
 |
| |
 |
|
|
 |
| |
| |
範例 35:狗追兔子的問題 |
|
| |
在座標平面上,兔子由(0,0)出發,以等速 q 沿著 x
軸向右逃跑,狗由(0,a)出發, a > 0,狗頭始終瞄準兔子,以等速 p 追兔子,請討論狗在何時可以追上兔子?
|
|
| |
《 解答 》 |
|
| |
設狗跑的路徑為 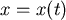 , ,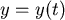 ,則有 ,則有
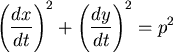 |
.........(1) |
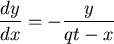 |
........................(2) |
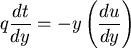 |
................(3) |
將(1)除以 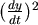 ,得 ,得 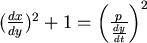 因此 因此
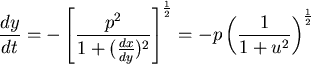 |
............(4) |
將(4)代入(3),得
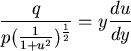 |
................(5) |
以  表 表 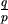 ,(5)寫成 ,(5)寫成 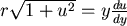
分離變數法: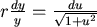
積分: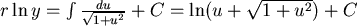
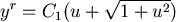
初始值: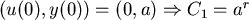
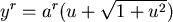
因此
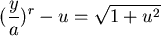
兩邊平方後整理: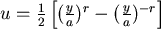 , ,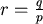 , ,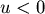 。 。
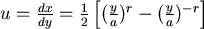
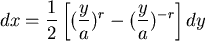 |
.............(6) |
第一種情形: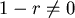 , ,
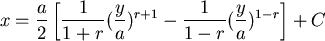
初始值: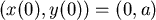 ,得到 ,得到 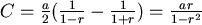 ,那麼 ,那麼
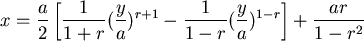
如果 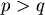 則 則 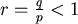 ,令 ,令 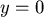 ,得出 ,得出 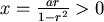 。 。
狗在 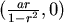 追上兔子,需時 追上兔子,需時 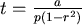 。 。
如果 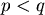 則 則 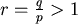 。當 。當 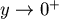 , ,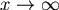 ,狗追不上兔子。 ,狗追不上兔子。
第二種情形: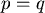 , ,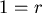 。 (6)式變成 。 (6)式變成 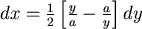
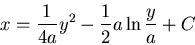
初始值: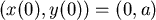 ,得 ,得 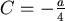 ,則 ,則
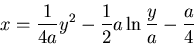
當 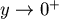 時,同樣有 時,同樣有 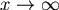 ,因此狗也追不上兔子。 ,因此狗也追不上兔子。
不過,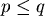 狗追不上兔子是常識。 狗追不上兔子是常識。
本文參考:Agnew, Differential Equation 2nd
ed. P.51. Problem 2.456。
|
|
| |
|
|
| |
About
This document |
|
| |
This document
was generated using the LaTeX2HTML
translator Version 2K.1beta (1.47)
Copyright © 1993, 1994, 1995, 1996, Nikos
Drakos, Computer Based Learning Unit, University
of Leeds.
Copyright © 1997, 1998, 1999, Ross
Moore, Mathematics Department, Macquarie
University, Sydney.
The command line arguments were:
latex2html -local_icons -white -notransparent
canswer02-html.tex
The translation was initiated by Shu Cheng-chou
on 2003-05-13
|
|
|
| |
|
| |
|
|
| |
|
 |















