|
設底面的圓半徑為  ,高為 ,高為 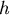 ,體積固定為 ,體積固定為 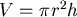 ,考慮最簡單的情形,在體積固定的情形之下,鐵罐的表面積愈小所需的材料便愈少,花費也就愈少,這麼一來問題便簡化為在 ,考慮最簡單的情形,在體積固定的情形之下,鐵罐的表面積愈小所需的材料便愈少,花費也就愈少,這麼一來問題便簡化為在
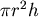 固定為 固定為 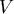 的情況下, 求表面積 的情況下, 求表面積 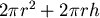 的最小值,這可以用微積分來處理,不過在此用算幾不等式比較快: 的最小值,這可以用微積分來處理,不過在此用算幾不等式比較快:
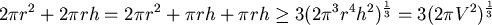
等號成立於 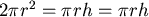 ,即 ,即 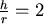 。觀察此一結果, 。觀察此一結果,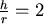 表示底面的圓直徑和高相等,這和我們日常生活中所見的罐子不太符合。 表示底面的圓直徑和高相等,這和我們日常生活中所見的罐子不太符合。
製造鐵罐的時候,上下底的圓其實是從鐵片上裁下來的,如圖一和圖二所示,所以裁出一片圓所需的鐵片面積分為圓的外接正方形和外接正六邊形的面積,半徑為 的圓其外接正方形面積為 的圓其外接正方形面積為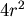 ,外接正六邊形的面積為 ,外接正六邊形的面積為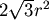 , ,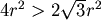 ,可見圖二中的方法較為節省。 ,可見圖二中的方法較為節省。
採用圖二的方法,則製作一個鐵罐所需的鐵片總面積為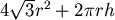 ,在體積 ,在體積 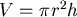 固定的情形下, 固定的情形下,
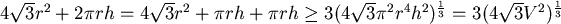 最小值發生在 最小值發生在 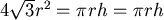 ,即 ,即 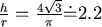 。 此結果比原先的結果稍稍接近日常生活中所見鐵罐的值,但還是有段差距。 。 此結果比原先的結果稍稍接近日常生活中所見鐵罐的值,但還是有段差距。
製造鐵罐時除了有材料上的花費外,將鐵片焊接在一起也是有花費的,鐵罐的側面是將一長為 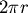 ,寬為 ,寬為 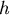 的長方形中的兩條寬焊接在一起而成,再焊接上下兩個圓鐵片便形成鐵罐,所以焊接的總長度為 的長方形中的兩條寬焊接在一起而成,再焊接上下兩個圓鐵片便形成鐵罐,所以焊接的總長度為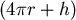 。 。
將單位面積的鐵片價格視為 1,若焊接單位長度需花費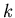 ,則製造一個鐵罐的花費為 ,則製造一個鐵罐的花費為 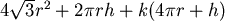 。在 。在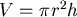 固定的情形下,求此花費的最小值。 固定的情形下,求此花費的最小值。 令 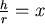 , ,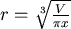 , ,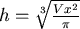 , ,
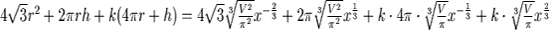 。 。
令此函數為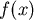 ,欲求 ,欲求 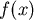 的最小值,取 的最小值,取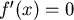 ,又 ,又 ,化簡可得 ,化簡可得 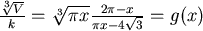 ,當 ,當 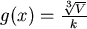 時, 時,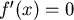 , 又 , 又 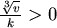 ,可知 ,可知 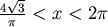
利用繪圖軟體將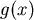 在 在 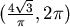 間的圖形繪出,如圖三所示, 間的圖形繪出,如圖三所示,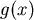 在 在 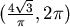 間從 間從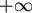 遞減到 0,所以一定可以找到唯一的 遞減到 0,所以一定可以找到唯一的 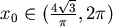 使得 使得 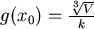 , ,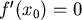 ,此 ,此 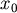 就是使 就是使 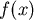 有最小值的點。 有最小值的點。
我們可以看出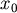 的值與 的值與 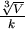 有關,當 有關,當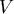 愈大或 愈大或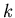 愈小則 愈小則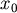 愈小,當 愈小,當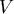 愈小或 愈小或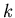 愈大則 愈大則 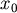 愈大,也就是說當一個鐵罐是以上述最經濟的方式製作時,若體積愈大或焊接的成本愈低,則其高和半徑的比例愈小,若體積愈小,或焊接的成本愈高,則其高和半徑的比例愈大,而高和半徑的比例介於 愈大,也就是說當一個鐵罐是以上述最經濟的方式製作時,若體積愈大或焊接的成本愈低,則其高和半徑的比例愈小,若體積愈小,或焊接的成本愈高,則其高和半徑的比例愈大,而高和半徑的比例介於
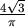 和 2π之間,是不適和日常生活中的觀察滿符合的呢?實際上,一般所見的罐子,其高和半徑的比大約在 2.2 到 3.8 之間,3.8
和 2π有段差距,這應該是因為 和 2π之間,是不適和日常生活中的觀察滿符合的呢?實際上,一般所見的罐子,其高和半徑的比大約在 2.2 到 3.8 之間,3.8
和 2π有段差距,這應該是因為 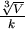 常大於某一正數,才使 常大於某一正數,才使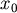 常小於 3.8。 常小於 3.8。
|















