| |
 |
| |
 |
|
|
 |
| |
| |
範例 30:蜂房問題 |
|
| |
蜂房的外觀呈正六角柱狀,你知道如何計算它的表面積嗎?
|
|
| |
《 解答 》 |
|
| |
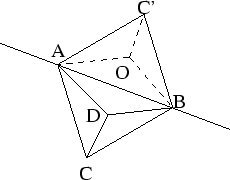
一個固定邊長 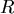 的正六角柱,上方被替換成三個交於一個公共點的菱形。如下圖所示: 的正六角柱,上方被替換成三個交於一個公共點的菱形。如下圖所示:
(先將四面體ABCD截下,再將 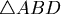 與  貼合,得到圖二,再對另外兩個四面體作同樣的動作,最後得到圖三)柱的底面是空的,而總體積會是一個常數,不妨設成
 ,如果我們假設  ,那麼此柱體的表面積  會是以下的形式:
並證明當 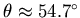 時, 時, 會有最小值。 會有最小值。
該如何計算蜂房(圖三)的表面積呢?
由題目所述的過程中可以清楚地了解:表面積為六角柱的柱面面積(1)減掉六個小三角形(2)再加上三個菱形面積(3)。由於它是"正"六角柱構成的,所以我們可以只算一小部分的表面積即可
- 體積
 ,底面積為六個小的正三角形組成,邊長為 ,底面積為六個小的正三角形組成,邊長為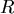 ,所以底面積 ,所以底面積
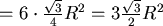 ,得到柱高 ,得到柱高 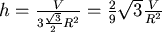 因此周圍的表面積 因此周圍的表面積 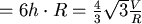
- 切掉的六個小三角形面積需要注意一下,因為
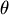 是最後最高點與底面和最矮邊長的夾角,事實上 是最後最高點與底面和最矮邊長的夾角,事實上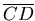 的長度等於圖二中 的長度等於圖二中 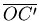 的長度,用側面圖來看就可以很清楚地知道關係了(圖六)所以 的長度,用側面圖來看就可以很清楚地知道關係了(圖六)所以 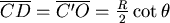 ,因此六個小三角形的總面積為 ,因此六個小三角形的總面積為
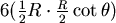
圖五 |
圖六 |
 |
|
- 三個菱形的總面積
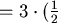 兩對角線之積 兩對角線之積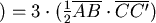 = =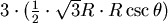 = =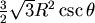 (見圖七、八) (見圖七、八)
所以蜂房的表面積=(1)–(2) + (3)=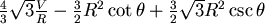 進一步地,我們發現總表面積呈現一個和
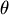 有關的函數(因為 有關的函數(因為  和 和 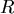 都固定了),並且 都固定了),並且 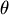 在 在 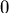 ~ ~ 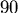 度之間 度之間 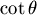 與 與 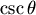 是連續可微分的, 是連續可微分的,
因此我們可利用微分的方法找到 的極值: 的極值:
註:圖一中四面體ABCD這一塊切下的同時,繞軸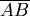 旋轉 旋轉 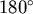 ,使 ,使 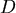 與 與 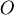 重合,就得到圖三。 重合,就得到圖三。
|
|
| |
|
|
| |
About
This document |
|
| |
This document
was generated using the LaTeX2HTML
translator Version 2K.1beta (1.47)
Copyright © 1993, 1994, 1995, 1996, Nikos
Drakos, Computer Based Learning Unit, University
of Leeds.
Copyright © 1997, 1998, 1999, Ross
Moore, Mathematics Department, Macquarie
University, Sydney.
The command line arguments were:
latex2html -local_icons -white -notransparent
canswer13-html.tex
The translation was initiated by Shu Cheng-chou
on 2003-05-14
|
|
|
| |
|
| |
|
|
| |
|
 |















