|
|
 |
| |
 |
|
|
 |
| |
| |
 多項式》 多項式》 |
|
| |
範例 03:實係數多項式區間中根的個數 |
|
| |
一個實係數多項式,我們要如何知道在某一個區間裡出現了幾個實根呢? |
|
| |
《 解答 》 |
|
| |
讓我們來看看下面的方法(Sturm的發明)
給一個實係數多項式  ,先假設 ,先假設  ,(即 ,(即 無重根) 無重根)
設  , , 
且  , , 。 。
因為  ,所以我們得到的最後一個 ,所以我們得到的最後一個 是非零的常數, 是非零的常數,
我們稱 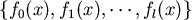 是 是 的Sturm數列。 的Sturm數列。
我們定義 是 是  正負號變化的次數。 正負號變化的次數。
例如: 的Sturm數列是 的Sturm數列是  那 那 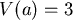
假設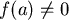 , , ,則 ,則  在 在 出現根的個數等於 出現根的個數等於
現考慮下列三種情形:
1.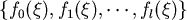 中不可能有連續為 0 的情形產生。 中不可能有連續為 0 的情形產生。
因為如果  ,則 ,則  (by (*)), (by (*)),
而導出  (但假設 (但假設 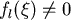 ) )
2.如果 , ,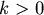 ,由(*)可知 ,由(*)可知 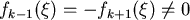 , ,
取足夠小的 使得符號列表如後: 使得符號列表如後:
由表可知 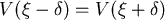
3.如果  , ,  ,那麼 ,那麼  。 。
假設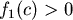 , ,
或假設
由表可知 
所以我們可以知道如果在  出現一個根時, 出現一個根時,
所以 在 在 根的個數是 根的個數是 舉個例子來看看吧!
 有幾個實根? 有幾個實根?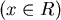
 , , , ,
 , , , , , ,
 , ,
當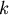 很大時 很大時
 , ,

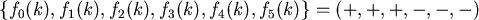
,
 ,所以 ,所以 有3個實根。 有3個實根。
(取材自項武義所著微積分,A Concise Introduction to Calculus,
World Scientific, 1995)
|
|
| |
|
|
| |
About This
document |
|
| |
This document was
generated using the LaTeX2HTML
translator Version 2K.1beta (1.47)
Copyright © 1993, 1994, 1995, 1996, Nikos
Drakos, Computer Based Learning Unit, University
of Leeds.
Copyright © 1997, 1998, 1999, Ross
Moore, Mathematics Department, Macquarie University,
Sydney.
The command line arguments were:
latex2html -local_icons -white -notransparent
canswer27-html.tex
The translation was initiated by Shu Cheng-chou
on 2003-05-26
|
|
|
| |
|
| |
|
|
| |
|
 |















