| |
 |
| |
 |
|
|
 |
| |
| |
範例 28:血液在血管中的流動 |
|
| |
在人體中,血液藉由動脈、靜脈、微血管來輸送,從心臟出發到達各組織或器官再返回心臟,在這個過程當中所需的能量越少,心臟的負荷就越小,血液在血管中除了受重力作用之外,也受到黏滯力的影響,你知道血管的夾角多少時,才能使血液所受到的黏滯力最小嗎?
|
|
| |
《 解答 》 |
|
| |
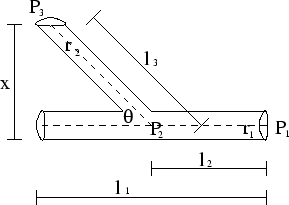
如圖所示,有條血管半徑為 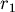 ,長度為 ,長度為 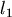 , ,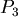 處有一器官,與此血管距離為 處有一器官,與此血管距離為 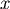 。需要一條半徑為 。需要一條半徑為 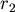 的血管連接到主血管來獲得血液,請問兩血管的夾角多少時,才能使血液由 的血管連接到主血管來獲得血液,請問兩血管的夾角多少時,才能使血液由 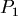 經 經 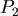 到 到 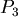 所受到的黏滯力最小? 所受到的黏滯力最小?
根據Poiseuille's law,當血管長度為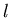 ,半徑為 ,半徑為  時,血液在血管中所受的黏滯力為 時,血液在血管中所受的黏滯力為 ,其中α為比例常數。血液由 ,其中α為比例常數。血液由 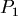 到 到 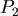 所受的黏滯力為 所受的黏滯力為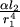 ,由 ,由 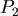 到 到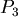 所受的黏滯力為 所受的黏滯力為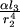 ,所以由 ,所以由 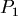 經 經 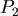 到 到 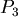 所受總力 所受總力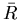 為: 為:
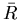 為 為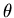 的函數, 的函數,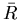 的極值發生在 的極值發生在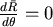 。 。
由於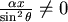 。所以 。所以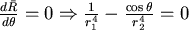 ,即 ,即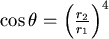 令 令 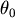 滿足 滿足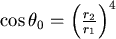 ,當 ,當 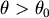 時, 時,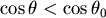 , ,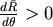 當 當 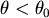 時, 時,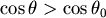 , ,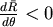 所以θ滿足 所以θ滿足 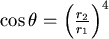 時, 時,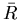 有最小值。 有最小值。
在R. Roseu所著的Optimality Principles in Biology(London:
Butterworth, 1967)當中提到,在大多情況之下,血管分支的角度的確符合上面所推導出來的結論。 |
|
| |
|
|
| |
About
This document |
|
| |
This document
was generated using the LaTeX2HTML
translator Version 2K.1beta (1.47)
Copyright © 1993, 1994, 1995, 1996, Nikos
Drakos, Computer Based Learning Unit, University
of Leeds.
Copyright © 1997, 1998, 1999, Ross
Moore, Mathematics Department, Macquarie
University, Sydney.
The command line arguments were:
latex2html -local_icons -white -notransparent
canswer20-html.tex
The translation was initiated by Shu Cheng-chou
on 2003-05-19
|
|
|
| |
|
| |
|
|
| |
|
 |















