|
|
 |
| |
 |
|
|
 |
| |
| |
 多項式》 多項式》 |
|
| |
範例 02:笛卡爾符號律 |
|
| |
首項係數為1的實係數多項式,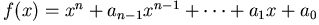
把係數依序排出,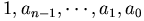 (中間如果有 0,就去掉不寫)看看從1到
(中間如果有 0,就去掉不寫)看看從1到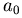 正負符號變了幾次,稱為 正負符號變了幾次,稱為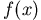 的變號數。例如:1,3,–5,–7,9
變號數是2; 1,–3,9,–4變號數是3。 的變號數。例如:1,3,–5,–7,9
變號數是2; 1,–3,9,–4變號數是3。
笛卡爾符號律是說:如果變號數是 k的話,那麼多項式f(x)的正實根的個數(重根要計以重數)一定是
k, 或k–2,或k–4,…,換句話說,正實根的個數小於或等於 k,但是可以與 k差一個偶數。
你知道這是為什麼嗎? |
|
| |
《 解答 》 |
|
| |
我們提供一個直接的看法,先假設
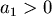 , ,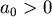 ,把 ,把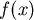 寫成 寫成
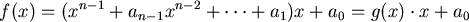
因為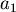 , ,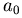 同號,所以 同號,所以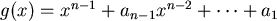 的變號數?是
k,因此由數學歸納法可以假設 的變號數?是
k,因此由數學歸納法可以假設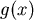 的正實根個數是
k 或 k-2 或 k-4,… 的正實根個數是
k 或 k-2 或 k-4,…
☆ 注意: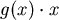 的正根和 的正根和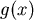 在一樣的位置。 在一樣的位置。
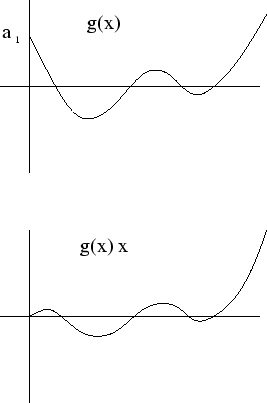
現考慮 由於 由於 是正的,所以圖形向上移動,正根的個數不會增加,只有可能減少,每一次減少都是偶數個。 是正的,所以圖形向上移動,正根的個數不會增加,只有可能減少,每一次減少都是偶數個。
如果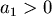 ,但是 ,但是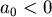 ,此時, ,此時,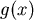 的變號數是
k–1。(比 的變號數是
k–1。(比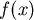 的變號數少1)再看上圖,考慮 的變號數少1)再看上圖,考慮 ,由於 ,由於 是負的,所以圖形要向下移動,剛開始移動一點點,現在0的右邊產生一個新的實根,由歸納法假設 是負的,所以圖形要向下移動,剛開始移動一點點,現在0的右邊產生一個新的實根,由歸納法假設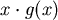 的正實根數是
k-1,或(k–1)–2,或(k–1)–4,…,由於 的正實根數是
k-1,或(k–1)–2,或(k–1)–4,…,由於 的正實根數會多
1,實根數變成 k,或 k–2,或 k–4,… 的正實根數會多
1,實根數變成 k,或 k–2,或 k–4,…
讀者可以嘗試寫下最後的證明。
|
|
| |
|
|
| |
About This
document |
|
| |
This document was generated
using the LaTeX2HTML
translator Version 2K.1beta (1.47)
Copyright © 1993, 1994, 1995, 1996, Nikos
Drakos, Computer Based Learning Unit, University
of Leeds.
Copyright © 1997, 1998, 1999, Ross
Moore, Mathematics Department, Macquarie University,
Sydney.
The command line arguments were:
latex2html -local_icons -white -notransparent
canswer36-html.tex
The translation was initiated by Shu Cheng-chou
on 2002-11-22 |
|
|
| |
|
| |
|
|
| |
|
 |















