|
經濟學上的Lorenz曲線是個很好的均值定理(Mean-Value
Theorem)的應用,比方說我們想要研究一個國家中的每個家庭所得收入的情形,我們可以用以下方式來了解:
- 先將所有住戶以所得由小到大排列
- 橫軸代表住戶的 "百分等級",縱軸所顯示的是 "累積所得" 佔總所得的百分比
如下圖:
如此一來,描繪出來的點畫成的曲線即為Lorenz Curve。
Lorenz Curve具有下面的幾個特質:
此曲線一定是遞增,並且凹口向上的圖形:(因為住戶數夠多,於是我們可將Lorenz
Curve畫得平滑些, 至少二階可微分)
不妨這樣子看:Lorenz Curve可以表示成 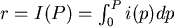 ,其中 ,其中 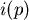 為百分等級為 為百分等級為 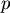 的住戶的所得佔全部所得的比例。 的住戶的所得佔全部所得的比例。
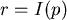 即此圖形的縱軸值 即此圖形的縱軸值
 , ,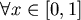 (微積分基本定理) (微積分基本定理)
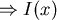 遞增 遞增
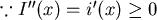 , ,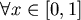 (因為排序方式是由小到大) (因為排序方式是由小到大)
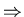 凹口向上。 凹口向上。
ESC(Equal-Share
Coefficient)
我們希望在Lorenz Curve一找到切線斜率為1的點,我們稱這個點是ESC(Equal-Share
Coefficient),簡記為  ,點 ,點  的收入正好和平均收入一樣(因為平均收入為(0,0)與(1,1)的割線斜率),因此它是一個很好的指標:在 的收入正好和平均收入一樣(因為平均收入為(0,0)與(1,1)的割線斜率),因此它是一個很好的指標:在
 以下的住戶所得比平均所得低,在 以下的住戶所得比平均所得低,在  以上的住戶所得比平均所得高。此點 以上的住戶所得比平均所得高。此點
 在Lorenz Curve上存在嗎? 在Lorenz Curve上存在嗎?
答案是肯定的,因為均值定理(Mean-Value Theorem)告訴我們:如果一函數在閉區間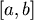 連續,在開區間 連續,在開區間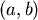 可微,則存在一點 可微,則存在一點 ,使得 ,使得 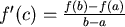 。用在Lorenz Curve上, 。用在Lorenz Curve上, 即為 即為 點。導函數 點。導函數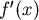 就是 就是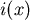 。並且:如果每個住戶所得不相等,則圖形的斜率 。並且:如果每個住戶所得不相等,則圖形的斜率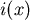 函數嚴格遞增,於是可以保證 函數嚴格遞增,於是可以保證
 唯一。 唯一。
Gini Coefficient
Gini Coefficient是一種衡量貧富差距大小的指標,我們可以想見:如果每個住戶的收入都一樣的時候,畫出來的Lorenz
Curve是(0,0)到(1,1)的直線,如果貧富差距愈大,則 Lorenz Curve就會離那條直線愈遠,Gini
Coefficient就是計算以下式子:
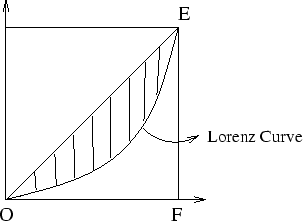
Lorenz Curve和對角線所包圍的面積與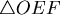 面積的比值 面積的比值
如果我們清楚Lorenz Curve的函數式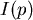 ,那麼Gini Coefficient就會是 ,那麼Gini Coefficient就會是
所以我們也可利用積分工具以得到Gini Coefficient。 |















