|
|
 |
| |
 |
|
|
 |
| |
| |
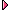 數列與級數》 數列與級數》 |
|
| |
範例 01:堆木板 |
|
| |
將長、寬、高及密度皆相同的均勻木板一片片往上堆,堆的時候遵循以下規則,木板的兩個側面須上下對齊,而上方的木板必須較下方的木板靠右或是重疊,
在維持不倒塌的情形之下,該怎麼堆才能使最上和最下兩塊木塊在水平方向的差距最大呢?又此時差距為多少? |
|
| |
《 解答 》 |
|
| |
最大差距發生在:從上方算下來總共 k 塊木板的重心剛好落在從上方算下來第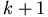 塊木板的最右端。如果最大差距的堆法不滿足上述,即對某個
k,上方算下來總共k塊木板的重心,在上方算下來第 塊木板的最右端。如果最大差距的堆法不滿足上述,即對某個
k,上方算下來總共k塊木板的重心,在上方算下來第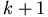 塊木板最右端的左側,此時可將第 塊木板最右端的左側,此時可將第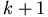 塊木板向左移動 塊木板向左移動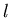 ,上方
k 塊木板向右移動 ,上方
k 塊木板向右移動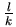 , ,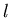 取夠小使得上方
k 塊木板的重心仍然不超過 取夠小使得上方
k 塊木板的重心仍然不超過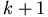 塊木板的最右端。此時一方面這 塊木板的最右端。此時一方面這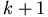 塊木板的重心維持不變,所以不會導致倒塌,而最上和最下的木板的差距可以變得更大。 塊木板的重心維持不變,所以不會導致倒塌,而最上和最下的木板的差距可以變得更大。
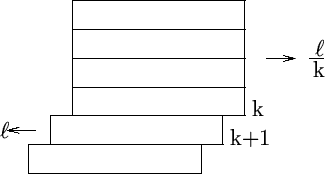

現在計算這最大差距的值,假設木板側面的長為 2,定最上一塊木板的右端水平坐標為
0,左方為正向,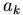 代表上方第
k 塊木板重心的水平坐標, 代表上方第
k 塊木板重心的水平坐標,
則 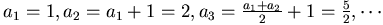
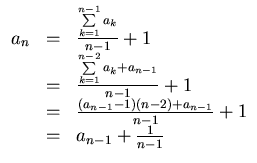
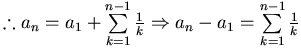 , 此為最大差距減2。
, 此為最大差距減2。
又 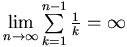 ,由此可看出,只要 ,由此可看出,只要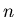 夠大(即木板夠多),此差距要有多大都辦得到,是不是有點出乎意料呢? 夠大(即木板夠多),此差距要有多大都辦得到,是不是有點出乎意料呢?
|
|
| |
|
|
| |
About This
document |
|
| |
This document was
generated using the LaTeX2HTML
translator Version 2K.1beta (1.47)
Copyright © 1993, 1994, 1995, 1996, Nikos
Drakos, Computer Based Learning Unit, University
of Leeds.
Copyright © 1997, 1998, 1999, Ross
Moore, Mathematics Department, Macquarie University,
Sydney.
The command line arguments were:
latex2html -local_icons -white -notransparent
canswer27-html.tex
The translation was initiated by Shu Cheng-chou
on 2003-05-21 |
|
|
| |
|
| |
|
|
| |
|
 |















