|
假設一半徑為 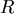 的球體,其密度 的球體,其密度 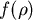 只與到球心 只與到球心 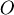 的距離 的距離 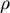 有關。假設有一質點 有關。假設有一質點 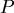 的質量為 的質量為 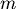 ,其到球心的距離為 ,其到球心的距離為 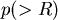 ,則球的質量為 ,則球的質量為 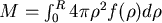 ,而把質量集中在球心後對質點 ,而把質量集中在球心後對質點 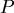 的引力,根據萬有引力定律且假設萬有引力常數(在適當的單位取法下)為 1,為 的引力,根據萬有引力定律且假設萬有引力常數(在適當的單位取法下)為 1,為  。Newton在考慮引力問題時,所遇到的問題之一就是,球體對質點的引力,是否和質量全集中在球心後對質點的引力是相等的。 。Newton在考慮引力問題時,所遇到的問題之一就是,球體對質點的引力,是否和質量全集中在球心後對質點的引力是相等的。
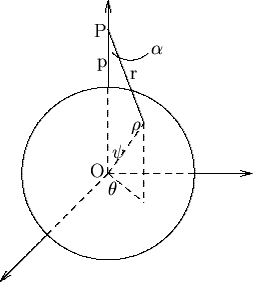
若質量不集中在球心,用球坐標,則球上一小體積 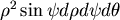 對距離 對距離  處的質點 處的質點 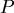 的引力在 的引力在 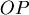 方向的分力為(因為對稱的關係,引力總和必在此方向) 方向的分力為(因為對稱的關係,引力總和必在此方向)
所以整個球體對質點 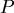 的引力為 的引力為
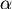 與 與  都和 都和 , ,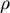 有關,所以該化成為它們的函數,才能開始積分。 有關,所以該化成為它們的函數,才能開始積分。
然而這樣的積分是積不出來的,據說這是Newton遲遲未能發表萬有引力原理的一個原因。
Newton後來還是把問題解決了,解決之道在於處理對  積分時(因此 積分時(因此 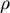 不變),把變數 不變),把變數  及 及 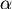 都換成變數 都換成變數  ,而變成對 ,而變成對  積分: 積分:
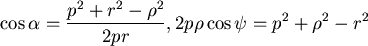
由後一式得(對  積分時, 積分時,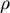 為常數) 為常數)
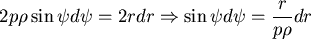
將這式子代入積分式得
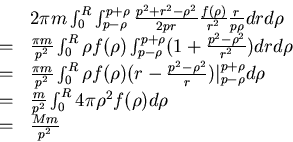
資料來源:取材自曹亮吉主編微積分, 歐亞書局出版
問題:如果質點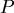 在球的內部,則結果如何?(補充部份)關於質點受到球體的重力,若是以重積分計算時,不妨設該點的位置在 在球的內部,則結果如何?(補充部份)關於質點受到球體的重力,若是以重積分計算時,不妨設該點的位置在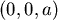 。球體球心在(0,0,0),半徑為 1。重力只需考慮 z 軸方向,大小是 。球體球心在(0,0,0),半徑為 1。重力只需考慮 z 軸方向,大小是
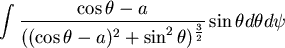
 從 0 到 2π是水平面上的輻角, 從 0 到 2π是水平面上的輻角, 從 0 到π,從z軸起算,相當 從 0 到π,從z軸起算,相當 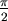 扣掉(北)緯度。(在北極是0而在南極是π) 扣掉(北)緯度。(在北極是0而在南極是π)
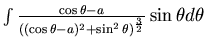
= 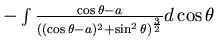
令 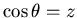 , ,
-原式 = 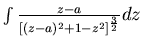
= 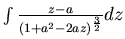
= 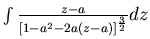
令 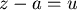 , ,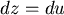
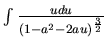
= 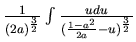
令 
得 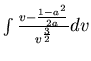
- (I)
如果 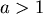 時, 表示質點在球的外部 時, 表示質點在球的外部
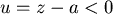 , ,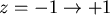 , ,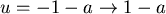 。 。
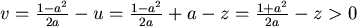 。 。
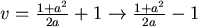 。 。
亦即 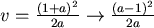 。 。
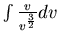 = = 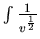
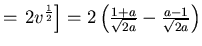
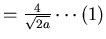
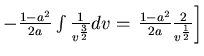
= 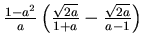
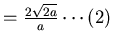
(1)+(2)得 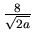 ,再乘以 ,再乘以 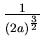 得 得 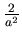 再乘上 再乘上 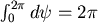 ,得 ,得 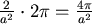 相當質量" 相當質量"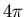 "集中在原點,對 "集中在原點,對 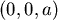 的重力。 的重力。
- (II)
如果 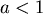 時,在所有計算中,牽涉到 時,在所有計算中,牽涉到 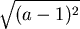 都要改為 都要改為 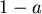
(1)式變成 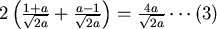
(2)式變成 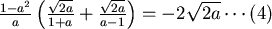
(3)+(4)得 0,亦即在球內部所受的重力為 0。
|















