|
給定坐標: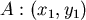 , ,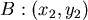 , , , ,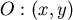 , ,
其中 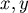 為變數,則: 為變數,則:
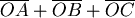
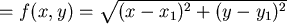
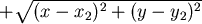 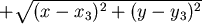
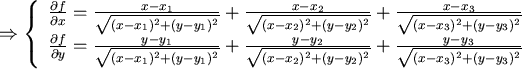
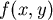 最小值可能發生之處為 最小值可能發生之處為 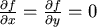 的點 的點
或偏導數不存在的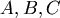 三點。 三點。
若 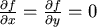 可解 可解 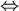 向量方程 向量方程
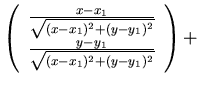 |
| ↓ |
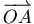 的單位向量 的單位向量 |
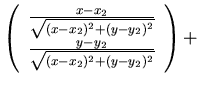 |
| ↓ |
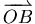 的單位向量 的單位向量 |
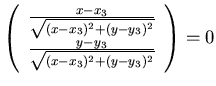 |
| ↓ |
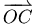 的單位向量 的單位向量 |
可解 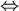 存在一點O使得 存在一點O使得 的單位向量+ 的單位向量+ 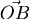 的單位向量 + 的單位向量 +  的單位向量 = 0向量。 的單位向量 = 0向量。
三個單位向量和為 0,則三個向量必互相夾 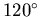 。 。
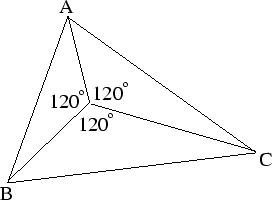
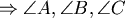 皆小於 皆小於 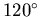 ;反之,若 ;反之,若 皆小於 皆小於 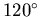 ,必可在A、B、C內部找到O點。 ,必可在A、B、C內部找到O點。
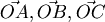 夾角皆為 夾角皆為 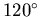
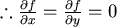 可解 可解  皆小於 皆小於 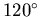 。 。
令  ,若 ,若  皆小於 皆小於 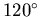 , ,
則 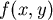 最小值發生在 A,B,C或 最小值發生在 A,B,C或 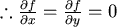 的解O上。 的解O上。
而 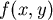 在A的值為: 在A的值為:
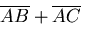
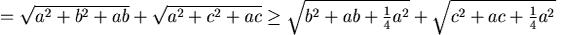
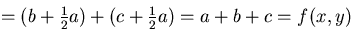
在O的值。 同理,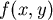 在B,C的值皆大於 在B,C的值皆大於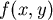 在O的值。 在O的值。
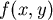 的最小值存在,可能發生的點僅 的最小值存在,可能發生的點僅 ,又在四點中,O的值最小, ,又在四點中,O的值最小,
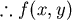 最小值發生在O, O滿足 最小值發生在O, O滿足 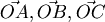 夾角 夾角 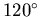
若  其中一角大於或等於 其中一角大於或等於 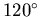
則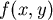 最小值可能發生在 最小值可能發生在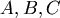 值分別為 值分別為 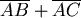 , ,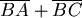 , ,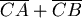 , ,
即 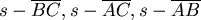 , ,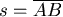 + + 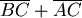 ,又角A為最大角, ,又角A為最大角,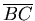 為最大邊, 為最大邊,
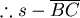 最小, 最小,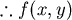 最小值發生在A。 最小值發生在A。
註:當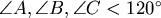 本題有一純幾何的做法作正 本題有一純幾何的做法作正  ,正 ,正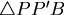 ,則 ,則 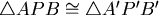 , ,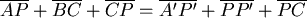
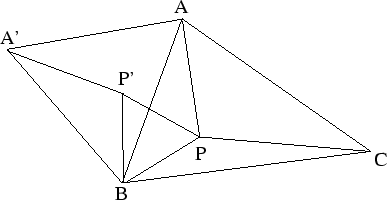
若要最小,則須選取 P 使得P, P' A', C在同一直線上。
此時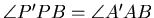 , A'APB為圓的內接四邊形。 , A'APB為圓的內接四邊形。
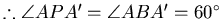
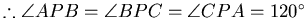
此一P點一般稱為費馬點
解法(二)(不用偏微分)
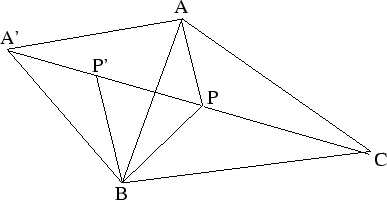
把問題改變一下,如圖:
在AP上找一點Q,使 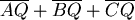 最小,先任取一點 最小,先任取一點 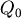 , ,
讓 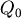 變動一點點到 變動一點點到 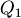 來看看,則到三點距離和的變化是 來看看,則到三點距離和的變化是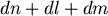 。 。
不妨設β是鈍角,α是銳角,則有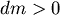 , ,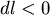 , ,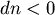 , ,
且 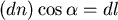 , ,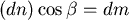 , ,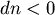 , ,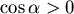 , ,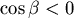 , ,
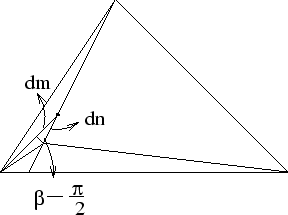
因此要求: 就得到 就得到 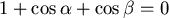 ,或 ,或 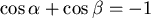 。 。
如果不要求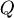 ,一定要在特定的直線AP上,但是仍然要求 ,一定要在特定的直線AP上,但是仍然要求 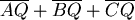 最小, 最小,
如此一來,當然有  , ,
因此 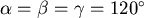 。 。
|















