| |
 |
| |
 |
|
|
 |
| |
| |
範例 43:傳播學的謠言擴散模型 |
|
| |
假設謠言就像傳染病,聽到的人一定要轉告給別人(沒有智者的八卦城市),則謠言的擴散會滿足Logistic模型:
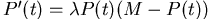
現假設在台灣某次選戰中,甲方為求勝選,決定造謠抹黑對方,但為了出奇制勝,決定在選舉前兩天才派人造謠,假設小城有10000選舉人口,且根據經驗,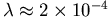 。試問: 。試問:
(1)如果甲方希望能在選舉當天有過半數的人知道這個謠言?他至少必須派出多少人的造謠部隊?
(2)如果甲願意將時間移為5天前?他又該怎麼做?
|
|
| |
《 解答 》 |
|
| |
何謂Logistic模型?
在了解Logistic模型之前,要先知道英國經濟學家馬爾薩斯(Malthus)在
1798 年發表的 "人口原理" 中,提出下述人口成長模型:
人口的成長率與總人口數成正比
寫成數學式則為: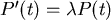 ,其中 ,其中 表示時間 表示時間 的人口數。 的人口數。
而比利時數學家 Verhulst 在 1840 年修正了馬爾薩斯的人口模型,他認為:
人口之成長不能超過由其地域環境所決定之某最大容量
於是提出下面的模型,通稱為Logistic模型:
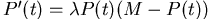 , ,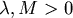 , ,
這方程的意思是: 在人口相對少時,基本上馬爾薩斯的模型是對的,
但當人口相當多時,人口成長率便會趨緩,而且越靠近人口上限 時,成長率越小。 時,成長率越小。
如何解微分方程?
利用分離變數法,記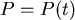 有 有  ,兩邊積分後, ,兩邊積分後,
左式  , ,
其中 是常數, 是常數,
而右式  , ,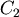 是常數,於是 是常數,於是
 , ,
 為常數, 為常數,
最後再化簡得  , , 為常數。 為常數。
若設初始條件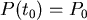 , , ,則 ,則 
回到原問題,此時 , ,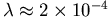 , ,
現在是希望找到在  時刻的 時刻的  為多少的時候會使得兩天之後的 為多少的時候會使得兩天之後的 值大於5000? 值大於5000?
即找 使得 使得 ,於是 ,於是  , ,
 , , 至少要派180人。 至少要派180人。
同樣地,若將時間改為五天的話,即解不等式:
 , ,
於是  , ,
∴他自己一人散佈即可。
|
|
| |
|
|
| |
About
This document |
|
| |
This document
was generated using the LaTeX2HTML
translator Version 2K.1beta (1.47)
Copyright © 1993, 1994, 1995, 1996, Nikos
Drakos, Computer Based Learning Unit, University
of Leeds.
Copyright © 1997, 1998, 1999, Ross
Moore, Mathematics Department, Macquarie
University, Sydney.
The command line arguments were:
latex2html -local_icons -white -notransparent
canswer46-html.tex
The translation was initiated by Shu Cheng-chou
on 2003-06-24
|
|
|
| |
|
| |
|
|
| |
|
 |















