| |
 |
| |
 |
|
|
 |
| |
| |
範例 39:四隻蒼蠅飛行問題 |
|
| |
有四隻蒼蠅A,B,C,D分別位於平面上的(1,1), (-1,1),
(-1,-1),(1, -1),之後牠們一起以每秒1單位的速度行動,行動的方式為:
A蒼蠅一直向著B蒼蠅靠近,
B蒼蠅一直向著C蒼蠅靠近,
C蒼蠅一直向著D蒼蠅靠近,
D蒼蠅一直向著A蒼蠅靠近,試問:
(1)四隻蒼蠅會在何處相遇?
(2)牠們多久會相遇?
(3)找出A蒼蠅的行動軌跡,並大致畫出。
(4)計算A蒼蠅從開始到相遇的路徑長。
(5)蒼蠅A會有什麼樣的生理反應?
|
|
| |
《 解答 》 |
|
| |
- (1)(2)
從物理相對運動的點來看A的行進方向始終和B的行進方向保持垂直,你可以想像蒼蠅移動了瞬間之後,方向就立即修正(參照圖一、二、三),由於四隻蒼蠅是做等速運動,所以每一時刻以四隻蒼蠅圍出來的四邊形會是正方形,(行進方向垂直加上等速)於是當時間愈久的時候,蒼蠅愈來愈靠近,正方形愈來愈小,最後會內縮成一點,這一點會是原點,這就是他們相遇的地方。此外,A靠近B是垂直方向靠近,所以從B蒼蠅看來,A還是以
1 單位 / 秒 的等速向B靠近,原來A、B的距離是 2 單位,因此需要 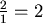 秒的時間四隻蒼蠅會相遇( 秒的時間四隻蒼蠅會相遇(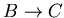 , ,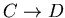 , ,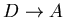 的推論都一樣,∴四隻會一起相遇) 的推論都一樣,∴四隻會一起相遇)
-
- (3)
我們將蒼蠅A的坐標位置用極坐標的方式表達,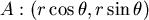 ,而B的位置就是 ,而B的位置就是  要注意的是: 要注意的是: 和 和 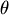 都是 都是 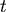 的函數 的函數 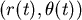
而A的速度是
此向量要與 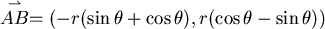 平行,於是(如果 平行,於是(如果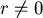 ) )

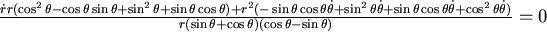
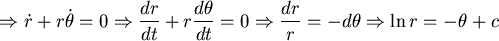
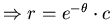 ,初始值 ,初始值 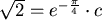 , , , ,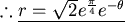 。 ( 。 ( 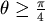 ) 其軌跡如下圖所示 ) 其軌跡如下圖所示
事實上我們必須注意到,在 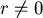 的情形下會有 的情形下會有 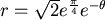 的推論,我們不妨用積分式算出 的推論,我們不妨用積分式算出
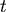 時刻走了多少路: 時刻走了多少路: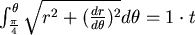 (等式右邊是速度乘上時間) (等式右邊是速度乘上時間)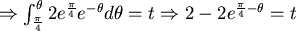 ,在 ,在 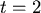 的時候, 的時候, ," ," 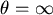 "。所以其實蒼蠅A的軌跡應為 "。所以其實蒼蠅A的軌跡應為
-
上述討論要表達的是說,加上  這一點是需要的,並且加上那一點後,軌跡還是連續的(可以想一下如何定義在端點的連續性) 這一點是需要的,並且加上那一點後,軌跡還是連續的(可以想一下如何定義在端點的連續性)
- (4)
由(3) 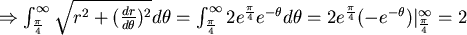
- (5)
由(3)得知在 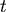 到 2 的時候, 到 2 的時候,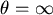 ,換言之,在之前已轉了無限多圈,於是蒼蠅會"頭昏"。 ,換言之,在之前已轉了無限多圈,於是蒼蠅會"頭昏"。
|
|
| |
|
|
| |
About
This document |
|
| |
This document
was generated using the LaTeX2HTML
translator Version 2K.1beta (1.47)
Copyright © 1993, 1994, 1995, 1996, Nikos
Drakos, Computer Based Learning Unit, University
of Leeds.
Copyright © 1997, 1998, 1999, Ross
Moore, Mathematics Department, Macquarie
University, Sydney.
The command line arguments were:
latex2html -local_icons -white -notransparent
canswer25-html.tex
The translation was initiated by Shu Cheng-chou
on 2003-05-19
|
|
|
| |
|
| |
|
|
| |
|
 |















