| 地表有一厚度固定的地層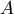 ,其下為地層 ,其下為地層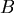 ,假設震波在 ,假設震波在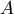 中前進的速率為 中前進的速率為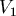 ,在 ,在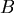 中為 中為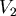 ,若 ,若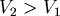 ,我們可以藉由測量震波來得知 ,我們可以藉由測量震波來得知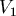 , ,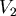 以及地層 以及地層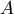 的厚度 的厚度 。 。
1.沿著地表傳送到乙,所需時間為  , ,
2.從甲出發,在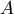 、 、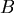 的交界處 的交界處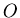 反射而到乙,所需時間為 反射而到乙,所需時間為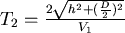
3.從甲出發,到達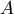 、 、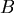 的交界處 的交界處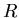 散射,沿著 散射,沿著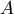 、 、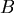 的交界處前進,到達某點 的交界處前進,到達某點 ,再散射到乙。 ,再散射到乙。
這樣的路線中有一條所花費的時間最少,此一路線在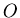 的兩側會對稱,考慮此種對稱的路線,如圖所示,則走此種路線所花費的時間 的兩側會對稱,考慮此種對稱的路線,如圖所示,則走此種路線所花費的時間
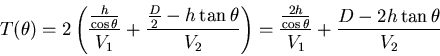
對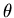 取導數, 取導數,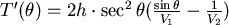 ,當 ,當 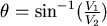 時, 時,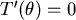 。當 。當 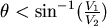 時, 時, , , 。當 。當 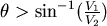 時, 時,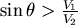 , ,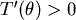 。所以 。所以 在 在 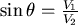 時有最小值 時有最小值 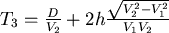 ,在此可看出 ,在此可看出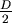 必須大於 必須大於 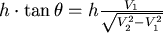 。也可看出為什麼要限制 。也可看出為什麼要限制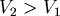 ,否則 ,否則 的最小值便是從甲到 的最小值便是從甲到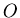 再到乙所花的時間 再到乙所花的時間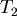 ,便得不到和 ,便得不到和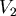 有關的數據 有關的數據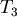 。 。
在甲處釋放震波後,在乙處可測得這三種震波到達乙所花的時間,該怎麼判別那個時間是那個震波抵達呢?
首先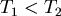 , ,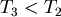 ,而 ,而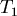 和 和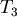 間的大小不一定,有以下關係: 間的大小不一定,有以下關係:
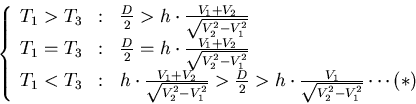
選取適當的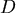 使得 使得 成立,便有 成立,便有 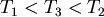 ,便可判別 ,便可判別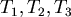 ,這樣的 ,這樣的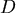 怎麼選呢?一開始任取一段距離 怎麼選呢?一開始任取一段距離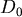 ,若此時只測得到2個震波( ,若此時只測得到2個震波(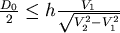 ),便將距離放大兩倍得 ),便將距離放大兩倍得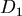 ,若能測得3個震波,則 ,若能測得3個震波,則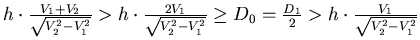 , , 式成立,可判別 式成立,可判別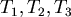 ,若依然只測得2個震波,重複同樣步驟即可。 ,若依然只測得2個震波,重複同樣步驟即可。
若在距離為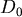 時能測得3個震波,取 時能測得3個震波,取 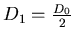 ,若在距離 ,若在距離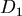 時只測得2個震波,可知 時只測得2個震波,可知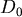 滿足 滿足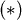 式,取 式,取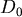 為距離即可,若在距離 為距離即可,若在距離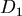 處仍測得3個震波,重複同樣步驟。 處仍測得3個震波,重複同樣步驟。
所以我們可以選取適當的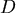 ,測出 ,測出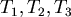 ,而 ,而
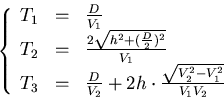
可解出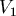 、 、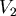 、 、 。 。
|















