| |
 |
| |
 |
|
|
 |
| |
| |
 積分問題》 積分問題》 |
|
| |
範例 23:撞球問題 |
|
| |
你知道撞球的時候球桿應該打在哪裡最好嗎?
|
|
| |
《 解答 》 |
|
| |
- 觀察1:
如果球桿打在撞球的中央(如圖A處)則球有速度,但是無旋轉的角速度,如此一來球和布會有摩擦, 布會壞掉,可見這不是最佳的點。 布會壞掉,可見這不是最佳的點。
◎球桿應打在讓球產生全滾動而不滑動,這是最佳的點。
- 觀察2:
若球一開始有滑動,不久球會開始滾動,滾速會增加,移動速度會減少,而質心速度會增加,到最後會有
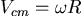 ,即滾動而不滑動,而摩擦力會消失。 ,即滾動而不滑動,而摩擦力會消失。
| 一些記號: |
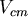 :球的質心速度 :球的質心速度 |
| |
ω:球轉動的角速度 |
| |
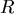 :球的半徑 :球的半徑 |
| |
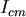 :球的轉動慣量 :球的轉動慣量 |
| |
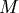 :球的質量 :球的質量 |
由物理學的角度來看,一剛性物體的角動量變化率等於力矩之和,寫成數學式即為 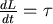 ,另外,角動量等於物體的轉動慣量乘上角速度,也就是說 ,另外,角動量等於物體的轉動慣量乘上角速度,也就是說 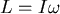 ,於是,用到撞球的例子上即為: ,於是,用到撞球的例子上即為:
註:
1.因為撞球的滾動是以貫穿球心的軸而轉動,所以其轉動慣量為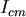 (質心) (質心)
2.力矩 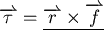 ,其中 ,其中 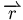 是轉動軸到施力點的方向向量,如果只關心力矩的大小,則 是轉動軸到施力點的方向向量,如果只關心力矩的大小,則 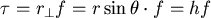
3.要達到全滾動而不滑動,則 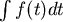 ,動量的變化率最後必須全部轉變為 ,動量的變化率最後必須全部轉變為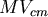 ,瞬間達成。 ,瞬間達成。
所以  最後,計算出 最後,計算出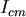 的值: 的值:
1.先計算空心球殼的轉動慣量:
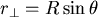 |
(球殼上的點到軸的距離) |
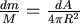 |
(均勻球殼, 質量與面積成正比) |
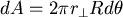 , ,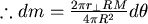 。 。
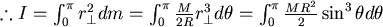
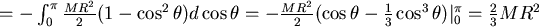
2.計算實心球殼的轉動慣量:
對球殼 r ,從O到R積分: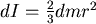 ,而 ,而
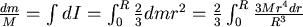
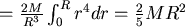
所以  結論:球桿應打在距球心高 結論:球桿應打在距球心高  處為最佳。 處為最佳。
☆補充:為何滾動而不滑動的時候會有 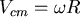 ? ?
∵滾動而不滑動
∴質心的位移等於弧長 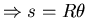 , ,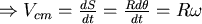
|
|
| |
|
|
| |
About This
document |
|
| |
This document was
generated using the LaTeX2HTML
translator Version 2K.1beta (1.47)
Copyright © 1993, 1994, 1995, 1996, Nikos
Drakos, Computer Based Learning Unit, University
of Leeds.
Copyright © 1997, 1998, 1999, Ross
Moore, Mathematics Department, Macquarie University,
Sydney.
The command line arguments were:
latex2html -local_icons -white -notransparent
canswer26-html.tex
The translation was initiated by Shu Cheng-chou
on 2003-05-21
|
|
|
| |
|
| |
|
|
| |
|
 |















