 積分問題》 積分問題》 |
| 範例 22:錄音帶 |
如果你曾注意過收音機帶動錄音帶的情形,相信你會發現在收聽(或者快轉)的時候,在左方的輪子會逆時針旋轉,以帶動磁帶,而原本在右方的磁帶地方就會被一直帶動,最後會繞到左方的輪子上。
現在我們考慮二個問題:兩個輪子磁帶半徑的變化率之比為多少? 如果我知道錄音帶從一開始(左方的輪子沒有磁帶,所有磁帶都在右方的輪子上)轉到一半
(左方的磁帶量=右方的磁帶量)時,需要一分鐘,並且輪 1 的轉速始終保持一定值,那麼錄音帶全部轉完的時候需要幾分鐘呢? |
| 《 解答 》 |
如果你曾注意過收音機帶動錄音帶的情形時,就會發現到,在收聽(或者快轉)的時候,在
1 處的輪子會逆時針旋轉,以帶動磁帶,而磁帶原本在 2 的地方就會被一直帶動,最後會繞到輪子
1 上。
現在我們想要考慮兩個問題:
- 記
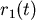 為1號輪子在 為1號輪子在 ![src="images_02/ex22_4.gif"]() 時刻所繞出的磁帶的半徑, 時刻所繞出的磁帶的半徑,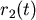 為2號輪子在 為2號輪子在 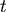 時刻磁帶形成圓形的半徑,它們會隨 時刻磁帶形成圓形的半徑,它們會隨 ![src="images_02/ex22_4.gif"]() 而變化,那麼兩半徑的變化率之比(即 而變化,那麼兩半徑的變化率之比(即
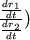 )為何? )為何?
- 如果我知道錄音帶從一開始(輪 1 沒有磁帶,所有磁帶都在輪 2上)轉到一半(輪 1的磁帶量=輪2的磁帶量)時,需要一分鐘,並且輪
1 的轉速始終保持一定值,那麼錄音帶全部轉完的時候需要幾分鐘?
第一個問題其實並不難,如果注意到磁帶的總量始終保持一定,另一個角度想就是兩磁帶所繞出的兩個圓形面積總和是固定的,於是會有
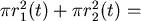 常數,對 常數,對 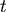 微分後得到 微分後得到
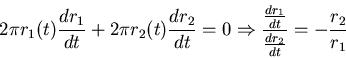
第二個問題我們可以試著用積分的方法解決,首先注意到由於轉速是一定(記為ω),所以半徑
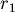 是和 是和 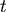 成正比,於是不妨令 成正比,於是不妨令 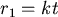 (比方說輪子每秒轉10圈,那麼一秒後半徑就多了10個磁帶的厚度,兩秒後半徑就多了20個磁帶的厚度)另外,我們同樣是以圓面積代表磁帶量,所以 (比方說輪子每秒轉10圈,那麼一秒後半徑就多了10個磁帶的厚度,兩秒後半徑就多了20個磁帶的厚度)另外,我們同樣是以圓面積代表磁帶量,所以
 (一分鐘時轉了總長的一半, (一分鐘時轉了總長的一半,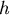 是一比例常數)欲解 是一比例常數)欲解 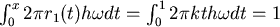 時的α值。 時的α值。
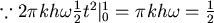
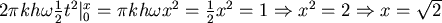
所以帶子全部轉完需要 分鐘。 分鐘。
|
|
| About This
document |
This document was
generated using the LaTeX2HTML
translator Version 2K.1beta (1.47)
Copyright © 1993, 1994, 1995, 1996, Nikos
Drakos, Computer Based Learning Unit, University
of Leeds.
Copyright © 1997, 1998, 1999, Ross
Moore, Mathematics Department, Macquarie University,
Sydney.
The command line arguments were:
latex2html -local_icons -white -notransparent canswer24-html.tex
The translation was initiated by Shu Cheng-chou
on 2003-05-19
|
|
|
|















