| 歷史上第一台求面積的儀器–「求積儀Planimeter」是在1814年由一位巴伐利亞的工程師赫爾曼發明。這台求積儀可能在操作上不很實際,
到了1854年由瑞士數學家阿穆斯勒(Jacob Amsler)發明的求積儀由於簡單又實用,從那時起一直沿用了一百多年以後才被電腦掃描取代。我手邊的這台求積儀是台大地理系在1970年從日本進口,它由兩根約二十公分長的桿子組成,第一根桿子稱為極臂(Pole
arm)臂的一端是極座(Pole)操作的時候要將極座先固定在紙上適當的位置。極臂的另一端是一個活動關節,連結到稱為描跡臂(Tracer
arm)的第二根桿子。描跡臂的頂端有一根針針尖朝下,在靠關節的這端有一個輪面與臂垂直的轉輪附在上面。(圖一)
操作的時候,(用手)持著針沿紙上一塊區域的邊緣掃描一圈,隨著針尖的掃描,輪子會前後轉動。針尖掃描一圈後,輪子轉出的刻度和描跡臂長度的乘積就是區域的面積。
為何藉著針尖的描繪可以讀出面積?我們注意到當針尖開始描圖的時候,輪子是順著針尖的大方向跟著前進的,此時,描跡臂掃過一片區域(圖二)。
慢慢地,針尖開始轉向了,輪子也開始倒退,描跡臂掃過另一片區域:輪子因為針尖的掃描而忽進忽退,進的時候描跡臂掃過的區域面積以正計之,退的時候以負計之,這此正負的總和就是原始曲線所圍出的面積。
因此,我們應該先行了解在描跡臂順向滑過一片區域的時候,這片區域的面積如何求得?
當描跡臂滑動的時候可以想成是以描跡臂所代表的線段重新參數化這片區域,線段上的位置坐標從關節算起以
s 表,關節的坐標是O,針尖的坐標是 l(l 是描跡臂的長度)。關節本身畫出一段圓弧,在 t
時刻的時候描跡臂所在的位置上任一點就賦予 s 和 t 兩個參數。
現在平面上有了兩組參數線,一組就是滑動的描跡臂,稱為 s 線,另一組是描跡臂上的各個點滑動的軌跡,稱為
t 線。
關節本身滑出的這段圓弧就是對應 s=0 的這條 t 線。
鄰近的 s 線和 t 線圍出小小的面積,但是為 t 線和 s 線並非垂直,我們不應把它當成是小長方形,而要看成是小平行邊形。
假設 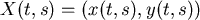 這一點的速度向量是 這一點的速度向量是 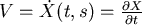 且在 且在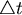 時間中移動了 時間中移動了 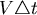 這一個小向量。 這一個小向量。
它與 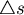 這一小段所形成的平行四邊形的面積就是 這一小段所形成的平行四邊形的面積就是 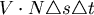 其中 其中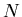 是描跡臂的單位法向量。 是描跡臂的單位法向量。
我們以內積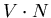 來表示 來表示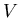 在 在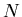 方向的投影的長度。 方向的投影的長度。
從微積分的經驗,我們以 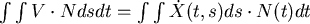 來計算面積,現在讓我們先積 來計算面積,現在讓我們先積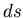 , ,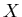 對 對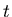 的微分暫時不管,所以會得到 的微分暫時不管,所以會得到 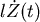 ,其中 ,其中 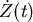 是描跡臂的中點,因為 是描跡臂的中點,因為 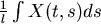 可說是位置的平均,再把微分擺回去就得出 可說是位置的平均,再把微分擺回去就得出
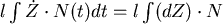 。積分的部分 。積分的部分 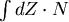 所表示的正是臂的中點在法向量方向的總位移,所以如果將轉輪附在描跡臂的中點,將輪的讀數乘以 所表示的正是臂的中點在法向量方向的總位移,所以如果將轉輪附在描跡臂的中點,將輪的讀數乘以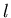 就是掃出的面積,當針尖繞一圈時,順向掃出的面積自動會扣除反向掃出的面積,所以輪上的淨讀數乘以 就是掃出的面積,當針尖繞一圈時,順向掃出的面積自動會扣除反向掃出的面積,所以輪上的淨讀數乘以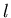 就是區域的面積。然而真正出廠的求積儀,輪子是附在關節處(見圖一)這是為了操作儀器的時候比較方便。但是這樣一來,輪子上的讀數不會改變嗎? 就是區域的面積。然而真正出廠的求積儀,輪子是附在關節處(見圖一)這是為了操作儀器的時候比較方便。但是這樣一來,輪子上的讀數不會改變嗎?
請看下面的解釋:假設輪子在關節處的位置向量是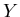 ,而在描跡臂中心的位置向量是 ,而在描跡臂中心的位置向量是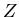 ,則有 ,則有
其中θ是描跡臂的角度,計算微分:
並且因為
所以
一般而言,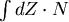 和 和 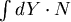 不會相等,可是我們實際上求的是環路積分, 不會相等,可是我們實際上求的是環路積分,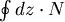 ,那麼只要θ不超過一百八十度, ,那麼只要θ不超過一百八十度,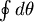 總是會等於零,這就證明了求積儀的操作與輪子所在的位置無關。 總是會等於零,這就證明了求積儀的操作與輪子所在的位置無關。
註:請參考大英百科Planimeter條及Courant and John微積分第二冊453頁。
|















