| 
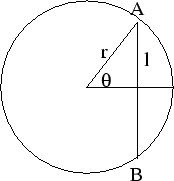
考慮一個更一般的問題,對一固定長 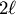 任何半徑
任何半徑  的圓皆可在圓內找到長為
的圓皆可在圓內找到長為 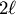 , 此弦所對應的弧之弧長
, 此弦所對應的弧之弧長 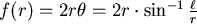 ,
,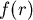 為
為  的遞減函數(
的遞減函數( )。若知此一結果,則原題目便可得證。 )。若知此一結果,則原題目便可得證。
現在證明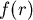 為
為 的遞減函數,
的遞減函數,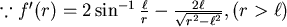 , ,
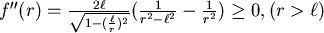 ,所以 ,所以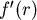 在 在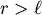 時為遞增。 時為遞增。
又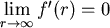
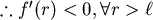 在 在 為遞減函數, 為遞減函數,
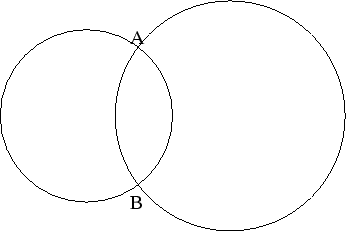
有了這個性質,我們可以再看另一個問題,球面上有A、B兩點,若從A點出發,在球面上沿一圓弧走到
B,要走那條圓弧才能使所走路徑最短呢?
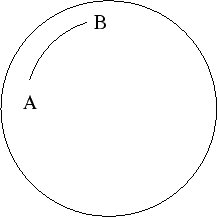
對這些圓弧來說,所對應的弦皆為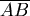 ,若弧長要越短,則半徑要越長,而球上半徑最長的圓為截平面通過球心的圓,所以
A 到 B 最短的圓弧為球心、A、B三點所在平面在球上所截出來的弧,此弧稱為由A到B的測地線(geodesic)事實上,測地線不只是在所有圓弧中長度最短,在球面上所有
A 到 B 的曲線中,測地線仍是長度最短的,因此,測地線可看成是球面上的直線。 ,若弧長要越短,則半徑要越長,而球上半徑最長的圓為截平面通過球心的圓,所以
A 到 B 最短的圓弧為球心、A、B三點所在平面在球上所截出來的弧,此弧稱為由A到B的測地線(geodesic)事實上,測地線不只是在所有圓弧中長度最短,在球面上所有
A 到 B 的曲線中,測地線仍是長度最短的,因此,測地線可看成是球面上的直線。 |
| This document
was generated using the LaTeX2HTML
translator Version 2K.1beta (1.47)
Copyright © 1993, 1994, 1995, 1996, Nikos
Drakos, Computer Based Learning Unit, University
of Leeds.
Copyright © 1997, 1998, 1999, Ross
Moore, Mathematics Department, Macquarie University,
Sydney.
The command line arguments were:
latex2html -local_icons
-white -notransparent canswer28-html.tex
The translation was initiated by
Shu Cheng-chou on 2003-05-21 |















