- A1: G-optimal design for simple linear model with efficiency function λ(x)=x+5
Type "Goptimal" (without the double quotes) to run the program.
The model is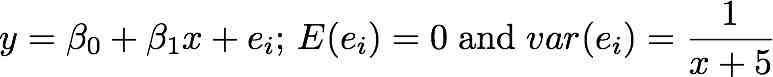
. - A2: E-optimal designs for the Michaelis-Menten model
Type "Eoptimal" (without the double quotes) to run the program.
The model is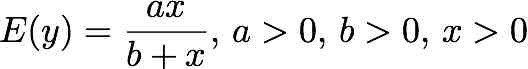
.
- R.-B. Chen, S.-P. Chang, W. Wang, and W. K. Wong. (2011) "Optimal Experimental Designs via Particle Swarm Optimization Methods." Technique report. [download]
- Wong, W. K. (1995). On the equivalence of D and G-optimal Designs in Heteroscedastic Models. Statistics & Probability Letters, Vol. 25, 317-321. [link]
- Dette, H. and Wong, W. K. (1999). E-optimal Designs for the Michaelis-Menten Model. Statistics & Probability Letters, Vol. 44, 405-408. [link]
Part B. Mixture Experiment
- B1: Minimally supported D and A-optimal designs for the linear, quadratic and cubic Scheffe's mixture polynomial models with q=3 factors on the regular q-simplex:
Type "run" (without the double quotes) to run the program.
The design experimental region is the regular q simplex,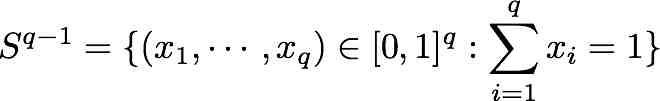
. The linear, quadratic and cubic Scheffe models with q = 3 are considered. The criteria are D- and A-optimal criteria.
- W. Wang, R.-B. Chen, C.-C. Huang, and W. K. Wong. (2012) "Particle Swarm Optimization Techniques for Finding Optimal Mixture Designs." Technique report. [download]
Part C. Locally D- and Ds-optimal Designs for Logistic Models
- C1: Locally D-optimal designs for simple linear logistic models
Type "Doptimal" (without the double quotes) to run the program.
The logistic model is defined as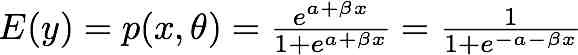
. - C2: Locally Ds-optimal designs for the parameter beta in simple linear logistic models
Type "Ds_optimal_b" (without the double quotes) to run the program.
The logistic model is defined as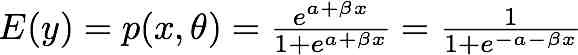
. - C3: Locally D-optimal designs for quadratic logistic models
Type "Doptimal" (without the double quotes) to run the program.
The model is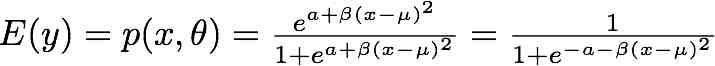
. - C4: Locally Ds-optimal designs for the parameters beta and mu in quadratic logistic models
Type "Dsoptimal" (without the double quotes) to run the program.
The model is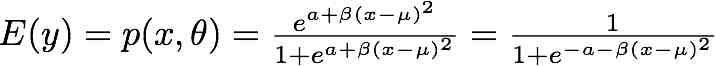
.
- J. Qiu, R.-B. Chen, W. Wang, W. K. Wong (2012) .“Using Animal Instincts to Design Efficient Studies,” Technique report. [download]
- Forniusa, E. F. and Nyquista, H. (2009) Using the Canonical Design Space to Obtain c-optimal Designs for the Quadratic Logistic Model. Communications in Statistics - Theory and Methods, Volume 39, 144-157
Part D. Locally designs for compartmental model
The model is
.- D1: Locally D-optimal design (Compartmental model D-opt)
Type "run" (without the double quotes) to run the program. - D2: Locally c-optimal design for the area under curve (Compartmental model AUC)
Type "run" (without the double quotes) to run the program. - D3: The locally c-optimal design for the time to maximum concentration (Compartmental model Time to max con)
Type "run" (without the double quotes) to run the program.
- J. Qiu, R.-B. Chen, W. Wang, W. K. Wong (2012) .“Using Animal Instincts to Design Efficient Studies,” Technique report. [download]
- Atkinson, A. C., Donev, A. N. and Tobias, R. D. (2007). Optimum Experimental Designs, with SAS. Oxford Statistical Science series, Vol. 34. 261-264
Part E. Locally D-optimal designs for 4-parameter Hill model
- E1: Locally D-optimal designs for 4-parameter Hill model (Hill model D-opt)
Type "run" (without the double quotes) to run the program.
The model is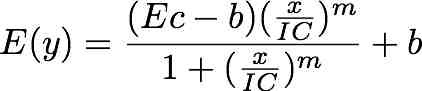
.
- J. Qiu, R.-B. Chen, W. Wang, W. K. Wong (2012) .“Using Animal Instincts to Design Efficient Studies,” Technique report. [download]
- Leonid A., Khinkis, L. A., Levasseur, L. Faessel, H. and Greco, W. R. (2003). Optimal Design for Estimating Parameters of the 4-parameter Hill Model. Nonlinearity in Biology, Toxicology and Medicine, Vol.1 #3, 363-377.
Part F. Locally D-optimal design for the double-exponential regrowth model
- F1: Locally D-optimal design for the double-exponential regrowth model (Double Exp model D-opt)
Type "run" (without the double quotes) to run the program.
The model is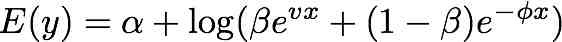
.
- J. Qiu, R.-B. Chen, W. Wang, W. K. Wong (2012) .“Using Animal Instincts to Design Efficient Studies,” Technique report. [download]
- Li G. and Balakrishnan N. (2011) Optimal designs for tumor regrowth models. J. Statist. Plann. Inf., 141, 644-654.
Part G. Two-parameter exponential model with type I right censored data
The probability density function and the corresponding survival function are
, where t is the observed value and x is the experimental condition for the observed data.- G1: Locally D-optimal design (Exponential type I censoring D-opt for survival paper)
Type "run" (without the double quotes) to run the program. - G2: Locally c-optimal design for the parameter β (Exponential type I censoring c-opt for survival paper)
Type "run" (without the double quotes) to run the program.
- J. Qiu, R.-B. Chen, W. Wang, W. K. Wong (2012) .“Using Animal Instincts to Design Efficient Studies,” Technique report. [download]
- Konstantinou, M., Biedermann, S. and Kimber, A. (2011). Optimal designs for two-parameter nonlinear models with application to survival models. Southampton Statistical Research Institute, University of Southampton.
Part H. Multivariate exponential and Poisson regression models
For the kth dose combination, xk= (xk1, …, xkM)’, the mean of this M-variable model is assumed to be
.- H1: Locally D-optimal design for Poisson regression model with M = 2
Type "run" (without the double quotes) to run the program. - H2: Locally D-optimal design for Poisson regression model with M = 3
Type "run" (without the double quotes) to run the program. - H3: Locally D-optimal design for Poisson regression model with M = 4
Type "run" (without the double quotes) to run the program. - H4: Locally D-optimal design for Poisson regression model with M = 5
Type "run" (without the double quotes) to run the program. - H5: Locally D-optimal design for exponential regression model with M = 3
Type "run" (without the double quotes) to run the program. - H6: Locally D-optimal design for exponential regression model with M = 4
Type "run" (without the double quotes) to run the program. - H7: Locally D-optimal design for exponential regression model with M = 5
Type "run" (without the double quotes) to run the program.
Disclaimer of Liability
These programs are provided here for evaluating the capability of particle swarm optimization for finding optimal designs. The codes should be used as they are and without any warranty.